6. Linked Structures - 2
1. Linked Structure와 Array는 대체로 시간복잡도가 비슷하지만, size, clear, destructor는 array가 빠름
그리고 Linked Structure에서 pointer 사용한다고 해서 이걸 크게 보기도 힘듬
LinkedStructure는 확장성 Scalability(Flexibility)에서 우위를 가짐 = Efficient memory management
=> linked structure : memory management efficient, array : memory efficient
Unsorted List
1. 맨 앞에다가 넣어야 시간복잡도 O(1) 나옴(Stack 이랑 비슷)
template <class ItemType>
void UnsortedType<ItemType>::appendItem(ItemType item) {
NodeType<ItemType>* tempPtr;
tempPtr = new NodeType<ItemType>;
tempPtr->value = item; // 새 노드에 값 할당
tempPtr->next = listData; // 새 노드의 next가 기존 리스트의 첫 노드를 가리도록 먼저 설정 후
listData = tempPtr; // listData가 새 노드를 가리키도록 설정
length++; // 리스트 길이 증가
}
2. Unsorted List는 length 변수 저장해놔서 size O(1) 나옴
Sorted List
3. Unsorted List랑 나머지는 다 똑같고 insertItem removeItem findItem 만 다시 정의
4. Sorted List라고 binary search 할 수 있는건 아님
Doubly Linked Structure
5. newNode가 먼저 팔을 뻗어야 함!!!
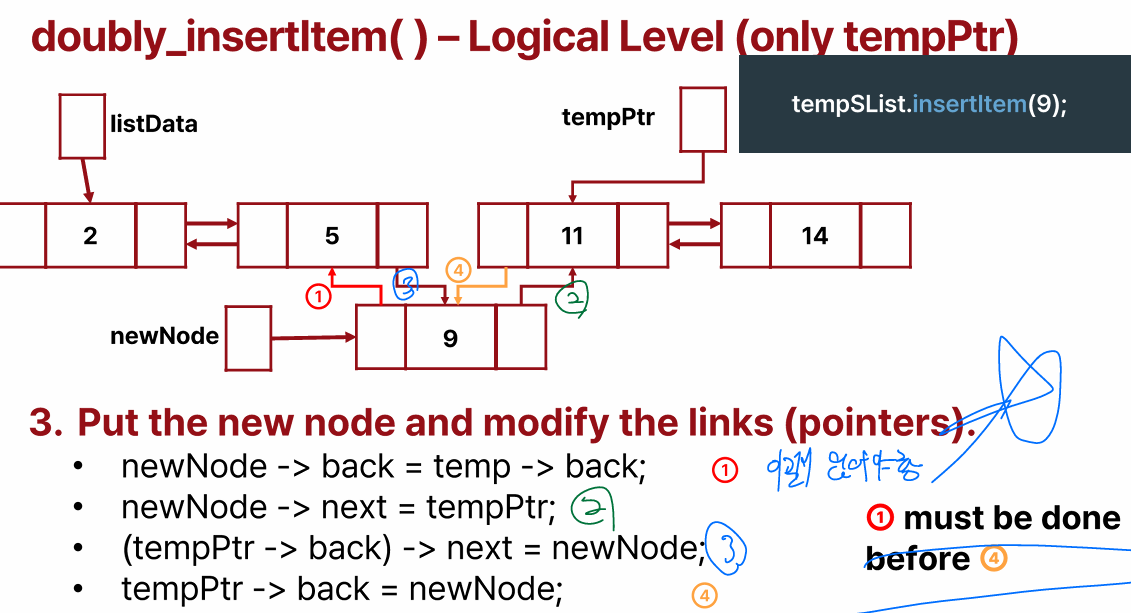
6. Doubly Linked Structures 예외 처리 ( remove 도 똑같)
- empty list에 insert 할때
- 첫번째로 insert 할 때
- 두번째로 insert 할 때
- 마지막에다가 insert 할 때
- 마지막 하나 전에다가 insert 할 때
Copy Instructor
7. Shallow copy는 dangling pointer문제 발생
- Shallow copy는 class data members 만 복사하고 pointed to data 포인터가 가리키는 실제 데이터는 복사하지 않음
- 반면에, Deep copy는 class data member 와 pointed to data 까지 모두 복사
8. deep copy 쓰려면 copy constructor 써야함
9. Copy constructor is used to make copies for pass by value.
10. Copy instructor는 passing, returning, initializing in a declaration 할 때만 쓸 수 있음
그래서 StackType<int> newStack = tempStack; 이건 deepcopy( 최초 선언이니까)
근데 StackType <int> newStack; newStack = tempStack; 이건 shallow copy ( = operator는 shallow copy를 하기 때문. 이걸 deepcopy하고싶으면 operator overloading 해야함)
7. Recursion
1. Direct recursion : 자기 자신 호출 / Indirect Recursion : 두개 이상이 서로 호출
2. Recursion
장점 : simple, 직관적
단점 : less efficient( 시간과 resource 면에서 다 )
ex) 재귀함수는 시간복잡도O( 2^N ) 인데 iteration은 O(N)임

3. combination 공식

4. 다음과 같이 쓰면 location의 기존 값을 잃게 됨.
NodeType<ItemType>* tempPtr = new NodeType<ItemType>;따라서 잃고 싶지 않으면 아래와 같이 써야함
NodeType<ItemType>* tempPtr = location; // 현재 노드의 위치를 tempPtr에 저장
location = new NodeType<ItemType>; // location에 새 노드를 생성
location->value = item; // 새 노드에 값 할당
location->next = tempPtr; // 새 노드의 next가 이전 노드를 가리키도록 설정
5. recursion 함수에선 pass by reference로 받아오는 게 중요
pass by reference는 연동!!!!!!!!!!!!!! 동기화 하는거임
6. Tail Recursion 꼴이 되면 그냥 반복문 써라 -> activation record가 계속 만들어지지 않도록
7. Inefficient Recursion : memoization 쓰기
8. 재귀가 깊어지지 않으면, 컴퓨터 메모리를 걱정할 필요 없이 재귀를 편하게 쓸 수 있다는 것
8. Trees
1. root는 level 0임
2. 높이(h)가 정해져있을때 최대 노드 수

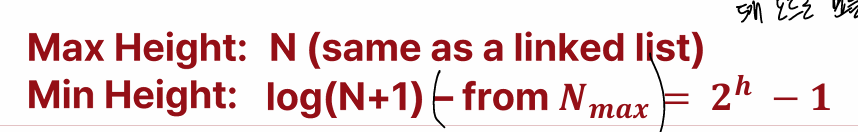
3. 트리 finditem 시간복잡도 O(N) : linkedstructure 형태일수도 있어서 (balanced 하면 O(logN))
4. deleteItem 하는법
- 갈림길을 찾는다
- The most right node in left subtree 나 The most left node in right subtree를 찾고
- replace data
- Delete The most right node in left subtree 나 The most left node in right subtree

Traversal 들은 하던 게 더 중요 위에 있는 거 보다
5. Inorder Traversal ㅅ

6. Preorder traversal < 형제보다 자식이 먼저임 : 뭉뚱그려서 볼 것 : 루트 - 왼쪽 트리 뭉텅이 - 오른쪽 트리 뭉텅이
7. Postorder traversal >
8.
| Inorder Traversal | 오름차순으로 트리 프린트하고싶을때 |
| Preorder Traversal | 트리 복사할 때 |
| Postorder Traversal | 트리 지울때(밑에서부터 지워야 하니까) |
Binary Tree Types
9. Full Binary tree : 모든 노드가 0이나 2개의 child node를 가짐
10. Complete Binary Tree: 위 쭉 채우고 -왼쪽에서 쭉 채운 트리
11. Perfect Binary Tree: 포화 이진 트리
12. 해당 노드의 left child에 가고 싶으면 tree.nodes[index*2 +1]
right child에 가고 싶으면 tree.nodes[index*2+2]
parent에 가고 싶으면 tree.nodes[(index-1)/2]
9. Heaps, Priority Queues, Graphs
Heap
1. Shape 하고 Order가 지켜져야 함
Shape : complete binary tree, Order : 자식보다 값이 커야 함
Heap Operations
2. Heap Insertion
우선 next bottom leftmost place(heap의 shape 성질 유지)에 node 만든 후 reheapup
Priority Queue
3. remove
제일 오른쪽 아래의 item을 root로 복사한 다음, 제일 오른쪽 아래의 노드는 지우고, reheapdown으로 재정렬
reheapdown할 땐 자식들 중 값이 큰 거랑 비교
template <class ItemType>
void HeapType<ItemType>::reheapDown(int root, int bottom_id) {
int maxChild;
int leftChild = root * 2 + 1;
int rightChild = root * 2 + 2;
// 왼쪽 자식이 존재하는 경우
if (leftChild <= bottom_id) {
// 왼쪽 자식만 존재하는 경우
if (leftChild == bottom_id) {
maxChild = leftChild;
}
// 왼쪽과 오른쪽 자식이 모두 존재하는 경우
else {
if (items[leftChild] <= items[rightChild])
maxChild = rightChild;
else
maxChild = leftChild;
}
// 부모 노드가 더 큰 자식 노드보다 작으면 교환
if (items[root] < items[maxChild]) {
std::swap(items[root], items[maxChild]);
reheapDown(maxChild, bottom_id);
}
}
}
9. Queue Big-O comparison
| Operation | enqueue | dequeue |
| Heap-Based | logN | logN |
| Sorted list based | N : 들어갈 곳을 찾고 넣어야 하므로 | 1 or N : 내림차순이냐 오름차순이냐에 따라 다름 |
| Binary search tree balanced skewed |
logN N |
logN N |
Trees
10. Terms
Adjacent nodes : 인접 노드
Complete graph : 모든 지점들끼리 연결된 그래프
Complete Directed Graph : 모든 지점들끼리 연결된 방향이 있는 그래프 : 길 N(N-1) 개
Complete Undirected Graph : 모든 지점들끼리 연결된 방향이 없는 그래프 : 길 N(N-1)/2 개
11. Adjacency Matrix vs List
Matrix : 밀집되어 있는 그래프에 좋음, 메모리 많이 잡아먹음,
12. BFS : 네비게이션 DFS : File 찾기
그러나, 길별로 weight가 있을때는 BFS보다 Dijkstra Algorithm 권장
13. Dijkstra Algorithm

첫번째 줄 : A에서 시작하는 걸로 할 때, 일단 다 무한대로 둠
두번째 줄 : A에서 갈 수 있는 B,C 의 weight를 씀 -> C가 B보다 3으로 짧음
세번재 줄 : C에서 갈 수 있는 B D E의 weight를 씀
ex) C를 들렸다가 B를 가는 것은 기존 값(10)보다 작으므로 기존 C의 값 + 추가 값으로 갱신
하고 보니까 이제 E가 세번째 줄에서 제일 짧음
네번째 줄 : E에서 갈 수 있는 D를 가봄. 오잉 근데 14로 기존의 값보다 큼. 더이상 갈 수 있는 데도 없음 -> 그 다음으로 작은 B로 감. 칸은 그대로 내려씀
다섯번째 줄 : B에서 갈 수 있는 C랑 D. B는 7+1 > 기존 3 보다 크므로 갱신 x, 그러나 D는 7+2 < 11 이므로 갱신
10. sort
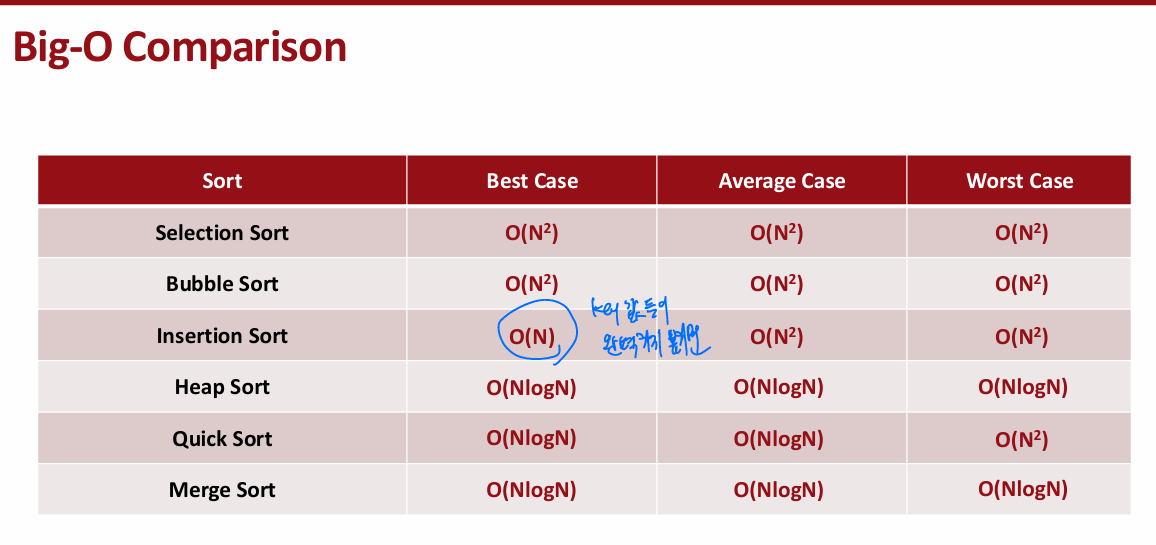
1. Selection Sort : 가장 작은거 찾고 앞으로 끄집어내고 계속 반복
2. Bubble Sort : 맨 뒤에 원소 본인보다 작은 원소를 만날 때까지 계속 swap
3. Insertion Sort: 맨 처음과 두번째의 원소만을 우선 정렬하여 정렬된 구간을 만들고, 세번째 부터는 정렬되지 않은 구간이라고 생각하고, 세번째 원소를 swap하며 정렬된 구간에 알맞게 삽입, 네번째 원소를 swap 하며 정렬된 구간에 알맞게 삽입
4. Heap Sort :
step 1. Unsorted Array를 Heap의 형태로 만든다. ->(N/2)logN 이므로 NlogN
step 2. Heap에서 reheapdown으로 큰거부터 하나씩 차출한다. NlogN
5. Quick Sort : 하나를 기준으로 잡고 이것보다 큰거끼리 모으고 작은거끼리 모으는 것.
평균적으론 NlogN 인데, 아다리 안맞으면 N^2됨
6. Merge Sort :
Hashing
7. Linear Probing : Deleted 로 둬야함 -> 그래야 keep finding 할 수 있음
8. Collision이 안 일어나게 하는게 제일 중요
9. 충돌을 최소화하는 법 : range를 늘리거나 키를 균등하게 분포시킨다.